Section 1.5
Transformations II: Composability, Linearity and Nonlinearity
Lecture Video
Intializing packages
When running this notebook for the first time, this could take up to 15 minutes. Hang in there!
"https://user-images.githubusercontent.com/6933510/108605549-fb28e180-73b4-11eb-8520-7e29db0cc965.png""https://user-images.githubusercontent.com/6933510/110868198-713faa80-82c8-11eb-8264-d69df4509f49.png""https://news.mit.edu/sites/default/files/styles/news_article__image_gallery/public/images/202004/edelman%2520philip%2520sanders.png?itok=ZcYu9NFeg"After you select your image, we suggest moving this line above just above the top of your browser.
The fun stuff: playing with transforms
This is a "scrubbable" matrix: click on the number and drag to change!
A =
#5 (generic function with 1 method)zoom =
pan = [
α=
2pixels =
Show grid lines
Circular Frame
321
480
Above: The original image is placed in a [-1,1] x [-1 1] box and transformed.
Pedagogical note: Why the Module 1 application = image processing
Image processing is a great way to learn Julia, some linear algebra, and some nonlinear mathematics. We don't presume the audience will become professional image processors, but we do believe that the principles learned transcend so many applications... and everybody loves playing with their own images!
Last Lecture Leftovers
Interesting question about linear transformations
If a transformation takes lines into lines and preserves the origin, does it have to be linear?
Answer = no!
The example of a perspective map takes all lines into lines, but paralleograms generally do not become parallelograms.
A nice interactive demo of perspective maps from Khan academy.

Challenge exercise: Rewrite this using Julia and Pluto!
Julia style (a little advanced): Reminder about defining vector valued functions
Many people find it hard to read
f(v) = [ v[1]+v[2] , v[1]-v[2] ] or f = v -> [ v[1]+v[2] , v[1]-v[2] ]
and instead prefer
f((x,y)) = [ x+y , x-y ] or f = ((x,y),) -> [ x+y , x-y ].
All four of these will take a 2-vector to a 2-vector in the same way for the purposes of this lecture, i.e. f( [1,2] ) can be defined by any of the four forms.
The forms with the -> are anonymous functions. (They are still considered anonymous, even though we then name them f.)
Functions with parameters
The anonymous form comes in handy when one wants a function to depend on a parameter. For example:
f(α) = ((x,y),) -> [x + αy, x - αy]
allows you to apply the f(7) function to the input vector [1, 2] by running f(7)([1, 2]) .
Linear transformations: a collection
Here are a few useful linear transformations:
shear (generic function with 1 method)In fact we can write down the most general linear transformation in one of two ways:
lin (generic function with 2 methods)The second version uses the matrix multiplication notation from linear algebra, which means exactly the same as the first version when
Nonlinear transformations: a collection
rθ (generic function with 1 method)Composition
trueComposing functions in mathematics
In math we talk about composing two functions to create a new function: the function that takes
We humans tend to blur the distinction between the sine function and the value of
If you look at the two sides of (sin ∘ cos )(x) ≈ sin(cos(x)) and see that they are exactly the same, it's time to ask yourself what's a key difference? On the left a function is built sin ∘ cos which is then evaluated at x. On the right, that function is never built.
Composing functions in computer science
A key issue is a programming language is whether it's easy to name the composition in that language. In Julia one can create the function sin ∘ cos and one can readily check that (sin ∘ cos)(x) always yields the same value as sin(cos(x)).
Composing functions in Julia
Julia's ∘ operator follows the mathematical typography convention, as was shown in the sin ∘ cos example above. We can type this symbol as \circ<TAB>.
Composition of software at a higher level
The trend these days is to have higher-order composition of functionalities. A good example would be that an optimization can wrap a highly complicated program which might include all kinds of solvers, and still run successfully. This might require the ability of the outer software to have some awareness of the inner software. It can be quite magical when two very different pieces of software "compose", i.e. work together. Julia's language construction encourages composability. We will discuss this more in a future lecture.
Find your own examples
Take some of the Linear and Nonlinear Transformations (see the Table of Contents) and find some inverses by placing them in the T= section of "The fun stuff" at the top of this notebook.
Linear transformations can be written in math using matrix multiplication notation as
.
By contrast, here are a few fun functions that cannot be written as matrix times vector. What characterizes the matrix ones from the non-matrix ones?
This may be a little fancy, but we see that warp is a rotation, but the rotation depends on the point where it is applied.
warp₂ (generic function with 2 methods)warp3 (generic function with 1 method)0.956225
-2.02129
6.21285
-4.73291
6.21285
-4.73291
Linear transformations: See a matrix, think beyond number arrays
Software writers and beginning linear algebra students see a matrix and see a lowly table of numbers. We want you to see a linear transformation – that's what professional mathematicians see.
What defines a linear transformation? There are a few equivalent ways of giving a definition.
Linear transformation definitions:
The intuitive definition:
The rectangles (gridlines) in the transformed image above always become a lattice of congruent parallelograms.
The easy operational (but devoid of intuition) definition:
A transformation is linear if it is defined by
The scaling and adding definition:
If you scale and then transform or if you transform and then scale, the result is always the same:
(
If you add and then transform or vice versa the result is the same:
(
The mathematician's definition:
(A consolidation of the above definition.)
for all numbers
The matrix

No not that matrix!
The matrix for a linear transformation
Once we have those, the linearity relation
is exactly the definition of matrix times vector. Try it.
Matrix multiply: You know how to do it, but why?
Did you ever ask yourself why matrix multiply has that somewhat complicated multiplying and adding going on?
0.781866
0.130273
0.781866
0.130273
Important: The composition of the linear transformation is the linear transformation of the multiplied matrices! There is only one definition of matmul (matrix multiply) that realizes this fact.
To see what it is exactly, remember the first column of lin(A) ∘ lin(B) should be the result of computing the two matrix times vectors
This is worth writing out if you have never done this.
Let's try doing that with random matrices:
-0.159731
-0.270888
-0.159731
-0.270888
lin(P*Q)
lin(P)∘lin(Q)
Coordinate transformations vs object transformations
642
960
If you want to move an object to the right, the first thing you might think of is adding 1 to the
Coordinate transform of an array
The original image has (1,1) in the upper left corner as an array but is thought of as existing in the entire plane.
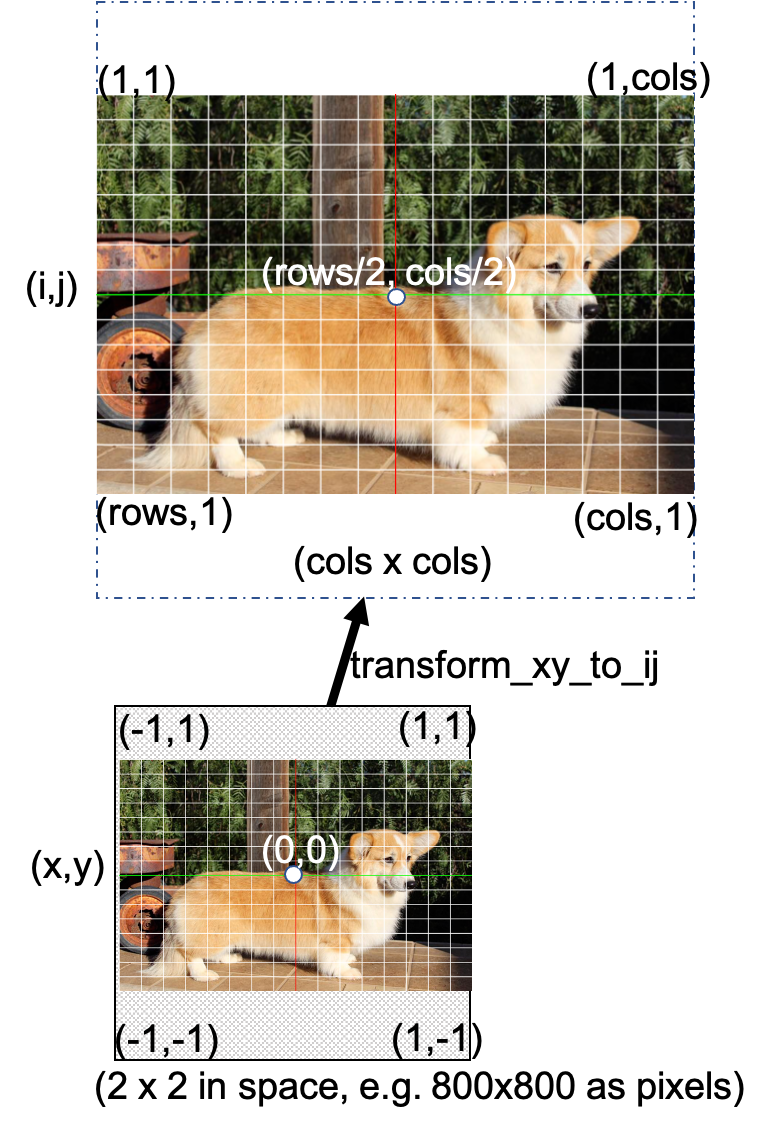
transform_ij_to_xy (generic function with 1 method)-0.995
0.995
-399
401
Inverses
If
and
This equation might be true for all
Example: Scaling up and down
0.559268
0.198111
0.559268
0.198111
true
true
We observe numerically that scale(2) and scale(.5) are mutually inverse transformations, i.e. each is the inverse of the other.
Inverses: Solving equations
What does an inverse really do?
Let's think about scaling again. Suppose we scale an input vector
Now suppose that you want to go backwards. If you are given
If we have a linear transformation, we can write
with a matrix
If we are given
Usually, but not always, we can solve these equations to find a new matrix
i.e.
so that
For
Inverting Linear Transformations
0.746831
0.713916
0.746831
0.713916
trueInverting nonlinear transformations
What about if we have a nonlinear transformation
In general this is a difficult question! Sometimes we can do so analytically, but usually we cannot.
Nonetheless, there are numerical methods that can sometimes solve these equations, for example the Newton method.
There are several implementations of such methods in Julia, e.g. in the NonlinearSolve.jl package. We have used that to write a function inverse that tries to invert nonlinear transformations of our images.
The Big Diagram of Transforming Images

Note that we are defining the map with the inverse of T so we can go pixel by pixel in the result.
Collisions

inverse (generic function with 3 methods)Why are we doing this backwards?
If one moves the colors forward rather than backwards you have trouble dealing with the discrete pixels. You may have gaps. You may have multiple colors going to the same pixel.
An interpolation scheme or a newton scheme could work for going forwards, but very likely care would be neeeded for a satisfying general result.
Appendix
1.0"https://user-images.githubusercontent.com/6933510/108605549-fb28e180-73b4-11eb-8520-7e29db0cc965.png"
"Corgis"
"https://images.squarespace-cdn.com/content/v1/5cb62a904d546e33119fa495/1589302981165-HHQ2A4JI07C43294HVPD/ke17ZwdGBToddI8pDm48kA7bHnZXCqgRu4g0_U7hbNpZw-zPPgdn4jUwVcJE1ZvWQUxwkmyExglNqGp0IvTJZamWLI2zvYWH8K3-s_4yszcp2ryTI0HqTOaaUohrI8PISCdr-3EAHMyS8K84wLA7X0UZoBreocI4zSJRMe1GOxcKMshLAGzx4R3EDFOm1kBS/fluffy+corgi?format=2500w"
"Long Corgi"
"https://previews.123rf.com/images/camptoloma/camptoloma2002/camptoloma200200020/140962183-pembroke-welsh-corgi-portrait-sitting-gray-background.jpg"
"Portrait Corgi"
"https://www.eaieducation.com/images/products/506618_L.jpg"
"Graph Paper"
black (generic function with 2 methods)with_gridlines (generic function with 1 method)